Measuring Ice Like NASA Does

Overview

One of the most important indicators of our warming climate is the extent and thickness of polar sea ice. Currently satellites measure the extent of polar sea ice but it takes more sophisticated equipment aboard a low-flying plane to actually measure the thickness of sea ice. This lesson will show students how this is done.

Objectives

Students should be able to use concepts of buoyancy and density to determine the thickness of a floating object indirectly.

Lesson Preparation

Many people are well aware that water expands as it freezes. The result of this is that the density of ice is approximately 10% less than that of fresh water. When an ice cube floats in a drinking glass, 10% of the ice is above the water level while 90% remains submerged.

If sea ice were simply flat pancakes of ice floating in fresh water scientists would have an easy time measuring the thickness of sea ice. NASA flies airplanes equipped with laser range-finding equipment (LIDAR) that can accurately measure the freeboard of sea ice – that is, how far above the water the ice sticks up. Using the 10% rule they could simply multiply this number by 10 to get the total thickness of sea ice. Reality, however, is never that simple. Several factors complicate the accurate measurement of sea ice thickness.

First, sea ice floats in a salty ocean that is MORE dense than fresh water. In addition, the salinity of the polar oceans can vary quite a bit in the vicinity of sea ice (depending on whether the sea ice is melting, freezing up, or neither). This matters because the buoyancy of ice (and therefore how much freeboard it has) depends on how dense the water is in which it floats.

Second, sea ice often has snow atop it (sometimes it even has seals, walruses, penguins, and polar bears). This common occurrence complicates the ice thickness calculations but it is still a manageable feat. Scientists can measure the thickness of snow atop ice by using a radar signal that penetrates the snow layer but is reflected off the ice. When this radar signal is combined with a laser altimeter the depth of the snow can be computed.

Third, sea ice is not typically a totally flat disk. Thickness can vary over relatively modest distances and pressure ridges can form when ice flows meet, driving thick ice up into the air which makes a miniature ice mountain range. In our experiment we will assume a uniform thickness of each chunk of ice.

Despite these and other complications, sea ice thickness can typically be computed with a fairly high degree of accuracy using models that take in account many of these variables. Ground-truthing (actually measuring the sea ice thickness by hand in certain places) helps scientists to check the accuracy of their models and adapt them to better represent the real world.

This laboratory experiment simulates the basic concepts around which sea ice models are formed. Students will measure surface features of simulated sea ice – just as the scientists do (though they do it from an airplane) – and then use these measurements to compute the overall thickness of the ice itself.

Procedure

As with many labs the set up is key here. Each group must construct a physical model of polar sea ice by making their own floating slab of ice. To do this the teacher must plan at least one day in advance and freeze some containers of water to make ice. In this sort of situation I like to get the students to help out and make their own containers of ice. This gives the students more “buy in” to the experiment. In Alaska we can just leave our containers outside overnight (most of the year) and they’ll free up nicely. An alternative to this is to borrow some space from the large freezers found in most schools’ cafeterias and make your ice there. Various shaped Tupperware containers work well and allow for different ice thicknesses.

On the day of the lesson obtain the containers of ice and thaw the edges in warm water – this should allow the ice slap to separate from the container. Just placing the container of ice in a tub of water should work fine.

Once the ice slab is floating in the tub you are ready to move on to the actual measurements. (If you’re doing extension 4 then “snow” should be gently added on top of the ice slab to form a fairly even layer. The thickness doesn’t really matter but it is important the “snow” is of a relatively uniform thickness throughout the slab.)

Measurements

Using a set of calipers (if available) or a cm ruler teams should measure the freeboard of the ice (it’s height above water). Measuring this at several locations around the rim and then averaging would be best. Be careful not to press down on the ice and set it bobbing – this will make your measurements both difficult and less accurate.

(Extension 1: Using a centimeter-ruler students should measure the thickness of the snow atop the ice. Making several measurements around the ice and averaging them would be more accurate.)

Calculations

When it is time to compute the predicted thickness of your “sea ice” it can be determined as follows. Since about 10% of an iceberg is above the water line it is simply a matter of multiplying the freeboard by ten:

dsubmerged ice = (dice above water) x 10

Here:
dsubmerged ice = thickness of the submerged ice
dice above water = thickness of ice above the waterline (the freeboard)

Remember, this is essentially how NASA calculates the thickness of sea ice (except they have computers to do the computations since there is a lot of sea ice at either pole!).

If you’re doing extension #1 then you have a slightly more complicated calculation ahead:

dsubmerged ice = ρsnow • dsnow + ρice • dice above water
/ ρwater

Where dsnow is the depth of the snow atop the ice.

The density terms here are denoted by the Greek letter rho, ρ:

ρwater= The density of fresh water is 1000 kg/m³ = 1.000 g/cm³.

ρice = The density of ice is about 917 kg/m³ = 0.917 g/cm³.

The density of the snow (real or fake) is ρsnow. This value is can be high variable. Here’s a chart from the National Snow and Ice Data Center (NSIDC) showing the densities of various types of snow.

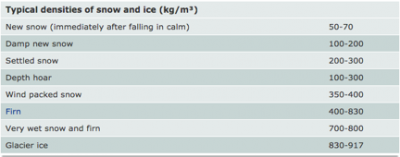
To convert these numbers to grams/centimeter³ simply divide the number shown by 1000.

If you are using potato flakes you should use a density of about 200 kg/m³. Even better yet, have your students figure out ahead of time the actual density of their snow (potato flakes). Real snow used for this part would most likely be a higher density. You may choose one of the values from the chart or simply match your snow type to the one that best matches it.

Extensions

1. Snow on top of the ice? (Originally this one was part of the main experiment. I took it out and put it here to make this more accessible for a wider range of students.) Snow is usually readily available in large quantities in Alaska during much of the school year. A great substitute for real snow is to use potato flakes which can be obtained in large quantities at low cost from your local warehouse store. Potato flakes layered alone make a great model for cold, dry snow, the type often found in polar regions. If you wish to give the “snow” more firmness then drizzle some water atop the flakes.

2. Change the density to mimic sea water. Groups should be encouraged to change the density of the water in the tubs and try the experiment again. Mix in up to 1.5 cups of salt into the water before adding the ice block. The increased salt content will raise the density of the now salt water, lifting the ice block higher out of the water. The data gathering proceeds as before however the final ice thickness calculation needs one correction:
   Substitute ρsalt water for ρwater.
   ρsalt water = The density of ocean water averages about 1027 kg/m³ = 1.027 g/cm³.
   If you mix in salt to the point where the water literally can’t take anymore salt it is said to be super-saturated. The density of a saturated salt water solution is 1200 kg/m³ = 1.200 g/cm³. The density of any kind of saltwater mixture can easily be found using a hydrometer.

3. How would the presence of animals atop the ice affect the calculation?
   Design an experiment to find out.
   Questions to answer: Suppose a number of walruses hauled out atop an ice pan. How can we account for their weight in our calculations? How does their presence affect the freeboard of the ice?

4. What happens to the water level when the ice completely melts?
   Design an experiment to find out.
   Hints: Note (and mark) the water level in a given tub as you begin the experiment. Leave the ice/tubs out overnight allowing the slabs to completely melt. Note the water level once the ice has completely melted. (It should be the same.) This is a great demonstration that shows how floating ice (be it sea ice or an ice shelf) does not affect sea level when it melts.

5. Explore the concept of negative feedback. Create two identical slabs of ice. Put enough blue food coloring into a tub of water so that the water is rather dark in color (just like ice free water at the poles). Place one ice slab in that container and another ice slab into one with regular (non-colored) water. Be sure to use the same amount of water for each tub.
   Place a heat lamp/incandescent bulb the same distance from each tub and keep track of how much time it takes to fully melt each one. How does the darker water affect the melt rate? How does the phrase “negative feedback” pertain to sea ice and what does it mean?

6. Investigate the difference between first year and multi-year sea ice? Why is the distinction important to the polar ecosystems? How does the loss of multi-year sea ice affect various marine organisms?

Additional more general extension questions:

What role does sea ice play in climate change?

What role does sea ice play in the ecology of the polar regions?

What animals rely on sea ice and how do they use it?

Resources

PolarTREC Program
PolarTREC’s website allows students to connect with teachers on polar expeditions. There, students can ask questions, follow particular expeditions, or investigate past expeditions. Teachers can access photographs and lesson ideas from a wide range of polar science topics. Like YouTube, it’s easy to lose a lot of time in this website!

National Snow and Ice Data Center
As the name suggests this website is essentially the world’s database for all data pertaining to snow and ice measurements (and there are tons!). The website has many links to research and current expeditions.

Derivation of formula for extension #1:

Buoyant force = total weight of iceberg system = weight of snow + weight of ice

FB = WTotal = Wsnow + Wice

ρwater • g • Vsubmerged ice = ρsnow • g • Vsnow + ρice • g • Vice above water

ρwater • dsubmerged ice = ρsnow<s/ub> • dsnow + ρice•x dice above water

dsubmerged ice = ρsnow • dsnow + ρice • dice above water / ρwater

Here V is volume and g is the acceleration due to gravity (9.8 m/s²).

Assessment

How did your group do? While holding the ice slab inside the tub, drain the water out. (For heavier slabs gently lift the slab of ice out first and then drain the water.) Now measure the actual thickness of the slab over several locations along the side (a good practice is to measure this as many times as you did the freeboard height). Calculate the average thickness of the ice and see how it compares to your prediction.

This assessment is also done for groups doing extension #1.

Summary

Many scientists use data from NASA’s airborne observatories to help predict what future sea ice will look like and its areal extent. This has very important implications to the ecology of the entire polar ecosystem as well as our global climate. Predicting how each will change in the future is something that has far-reaching consequences for humans and the organisms that inhabit these wonderful areas.

Author / Credits

PolarTREC Teacher Russell Hood. Russell can be contacted at <Hood_russell [at] asdk12.org>.

Note

I strongly recommend that teachers who use this lesson (or some modification of it) have their students write their measurements/calculations/conclusions, etc. in a science notebook.